OpenGL和3D图形一般都是基于向量和矩阵数学。…此处省略50字…
一旦有矩阵数据的基础,就可以继续学习OpenGL的教程了。
向量
数学向量是一种表示由多个部分组成的值的方法,可以用与表示一些带有大小和方向的事物。 要理解这些意思的最好方法是看一个例子。

这里有一个点,x=2, y=3。怎么用向量表示这个点?像这样:
2 3
就是这样。向量真的仅是表示值的方法,这个值由多部分组成,像我们刚才的情况就是表示一个由x和y 组成的一个点的位置。
多边形
现在这个有用吗?看,在OpenGL(和大多其他3D图像API)中,所有非常漂亮的东西都是作为一个多边形的几何被渲染。那么就会有人问这样一个问题:“在计算机里怎样表示一个多边形?” 我画这样一个三角形:

它可以用一个点的数组来表示。
这可以表示为向量的数组:
1 1 3 3 5 1
这可以被OpenGL使用,渲染一个多边形。 这个很重要,因为在3D图形中多边形被用于表示3D对象。
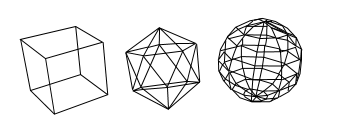
一个简单的无色立方提的3D模型仅仅一个大数字的数组。
const float cubeModel =
{
//Front
-1.f, -1.f, 1.f,
1.f, -1.f, 1.f,
1.f, 1.f, 1.f,
-1.f, 1.f, 1.f,
//Back
-1.f, -1.f, -1.f,
1.f, -1.f, -1.f,
1.f, 1.f, -1.f,
-1.f, 1.f, -1.f,
//Top
-1.f, 1.f, 1.f,
1.f, 1.f, 1.f,
1.f, 1.f, -1.f,
-1.f, 1.f, -1.f,
//Bottom
-1.f, -1.f, 1.f,
1.f, -1.f, 1.f,
1.f, -1.f, -1.f,
-1.f, -1.f, -1.f,
//Left
-1.f, -1.f, -1.f,
-1.f, 1.f, -1.f,
-1.f, 1.f, 1.f,
-1.f, -1.f, 1.f,
//Right
1.f, -1.f, -1.f,
1.f, 1.f, -1.f,
1.f, 1.f, 1.f,
1.f, -1.f, 1.f
};
上面这段代码用于渲染一个立方体。三一个一组的数字表示一个向量点,每4个向量的集合表示立方体 一个面的四个角。
3D向量
现在你已经知道了在2D空间的x/y坐标,那么在3D空间中又是怎么呢?在上面立方体模型的代码中, 每个点的第三个数字是z位置。左右方向是X的位置,上下方向是Y的位置,前后方向是Z的位置。
另为需要注意的是哪个是x,y和z的正方向。右边是X的正方向,左边是负方向。上边是Y的正方形,下边是负方向。朝向你的是Z的正方形,远离你的是负方向。这就是使用最多的“右手规则”。
向量算数
参考资料: